Oxygen and Fuels from In-Situ Resources on Mars
Customer: NASA, NextSTEP-2 ISRU
Technology: Solid Oxide Electrolysis Cells (SOEC), and Methane Synthesis Reactor

The NASA NextSTEP program is a continuation and expansion of the work OxEon has completed in association with JPL and MIT for the Mars 2020 mission, Project MOXIE (Mars OXygen In-situ resource utilization Experiment). Recognizing the need for a larger scale version of the solid oxide (SOXE) stack to meet ultimate NASA objectives, OxEon is developing a Mars manned-mission scale stack.
OxEon will demonstrate operation of the Mars manned-mission scale SOXE stack for co-electrolysis of CO2 and water vapor, and the technology to produce methane fuel from the SOXE produced synthesis gas (mixture of CO and H2). The scale of the stacks is such that four SOXE stack units will exceed the 2.3 kg/hr oxygen production rate requirement to produce 30 tons of propellant in the 435 day Mars landing to Earth launch, Mars Ascent Vehicle (MAV) propellant production window.
Status: Ongoing
Ask an OxEon Expert how we can help with:
- Ruggedized Hermetic SOEC Stacks Hydrogen/Oxygen/Syngas Production (SOEC)
- SOFC Stacks for Power Generation (SOFC)
- Systems Development Support
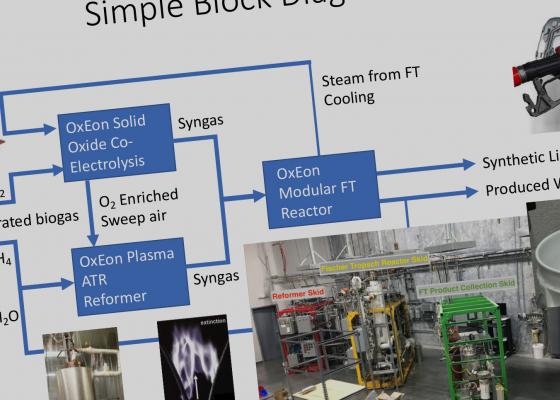
- Supporting Technologies for Liquid Fuel Production (Fischer Tropsch or Plasma Reformer Technologies)